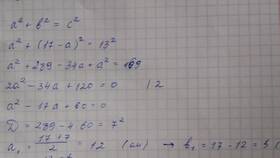В геометрии прямоугольного треугольника сумма длин катетов не имеет фиксированного значения, в отличие от определенных соотношений между сторонами. Рассмотрим основные свойства и формулы, связанные с катетами прямоугольного треугольника.
Содержание
В геометрии прямоугольного треугольника сумма длин катетов не имеет фиксированного значения, в отличие от определенных соотношений между сторонами. Рассмотрим основные свойства и формулы, связанные с катетами прямоугольного треугольника.
Основные понятия
Прямоугольный треугольник - это треугольник, у которого один угол равен 90°. Стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу - гипотенузой.
| Элемент треугольника | Обозначение |
| Первый катет | a |
| Второй катет | b |
| Гипотенуза | c |
Соотношение между сторонами
Основная связь между катетами и гипотенузой выражается теоремой Пифагора:
a² + b² = c²
Сумма катетов (a + b) может принимать различные значения в зависимости от конкретных размеров треугольника.
Примеры расчета
| Катет a | Катет b | Сумма катетов (a + b) |
| 3 | 4 | 7 |
| 5 | 12 | 17 |
| 6 | 8 | 14 |
Полезные соотношения
Хотя сумма катетов не постоянна, существуют интересные зависимости:
- Сумма катетов всегда больше гипотенузы (a + b > c)
- Разность катетов всегда меньше гипотенузы (|a - b| < c)
- Для подобных треугольников отношение сумм катетов равно коэффициенту подобия
Практическое применение
- В строительстве при расчете конструкций
- В навигации и геодезии
- При проектировании технических устройств
- В компьютерной графике
Таким образом, сумма катетов прямоугольного треугольника не является постоянной величиной, а зависит от конкретных размеров сторон. Важнее знать соотношения между сторонами, выраженные теоремой Пифагора и другими геометрическими закономерностями.
